Section 2: Wave Interaction
Section Learning Outcomes:
Section Key Terms:
Bored Already? Press the buttons to dive into applications!
Lesson 1: Superposition of Waves and Wave Interference
Superposition of Waves
Most waves are not as simple as the ideal cases considered in the previous sections like the basic water waves, which have perfect sinusoidal shapes. The majority of waves, such as real ocean waves or the waves produced by a guitar or violin string, appear more complex because they result from two or more simple waves that combine as they come together at the same place at the same time.
Imagine standing by the shore of a calm lake and throwing two stones into the water at different locations. As the waves generated by the stones spread outward, they eventually meet and overlap. At the points where the crests of the waves coincide, we observe an increase in the height of the water. This increase in the height of the water is known as . The waves reinforce each other, resulting in a higher wave. On the other hand, at points where a crest and a trough coincide, we observe a decrease in the height of the water. This is known as . The waves cancel each other out, resulting in a smaller wave or no wave at all. This phenomenon is called the and it is a fundamental principle in physics. According to this principle, when two or more waves meet at a given point in space, their individual displacements or disturbances add together algebraically to create a new wave pattern.
Wave Interference
Pure constructive interference occurs if the peaks of the two waves coincide with each other and arrive at the same point exactly in phase. When the waves are exactly in phase, the amplitudes of the individual waves to add, resulting in a new wave with a larger amplitude, but with the same wavelength, as seen in Figure 1.
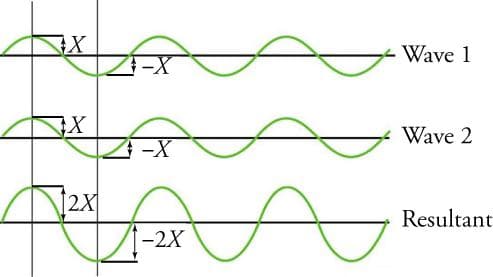
Figure 1: Pure constructive interference of two identical waves with amplitude X produces one with amplitude 2X, but the same wavelength (Texas Gateway).
If the peaks of one wave align with the troughs of another wave, they undergo pure destructive interference. The waves are exactly out of phase, causing the disturbances to add to zero, resulting in the wave disappearing as the waves completely cancel out each other, as seen in Figure 2.
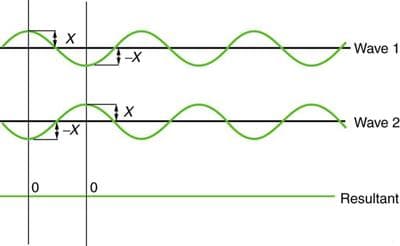
Figure 2: Pure destructive interference of two identical waves with amplitude X produces zero amplitude, or complete cancellation (Texas Gateway).
Now let's imagine you have a container of water with multiple layers of oil floating on the surface. When light from the surroundings hits these layers, it reflects off them, and some of the light waves bounce back to our eyes. When the light waves reflect off the layers of oil, they can interfere with each other. This means that the waves can either add up (constructive interference) or cancel each other out (destructive interference) in different regions.
In areas where the oil layers are of similar thickness and the light waves reflected from each layer align perfectly, they reinforce each other, resulting in brighter and more intense colours. You might notice vibrant and iridescent patterns in these regions. On the other hand, in areas where the oil layers are of different thicknesses, the reflected light waves can be out of sync and interfere in a way that they cancel each other out. This leads to regions with diminished or even no light, appearing darker or less colourful.
So, when you observe layers of oil floating on water, the thickness of each oil layer determines how the light waves reflecting off them interfere with each other. It creates regions of both bright and dark colors, forming a visually captivating pattern. This phenomenon, known as partial interference, helps us appreciate the complex and beautiful nature of light and waves. is the most common case of interference and occurs when the waves combine to form a new wave with an intermediate amplitude, as seen in Figure 3.
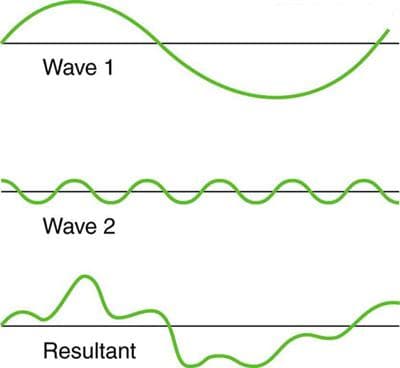
Figure 3: The superposition of non-identical waves exhibits partial interference (Texas Gateway).
Lesson 2: Standing Waves
Standing Waves
Imagine you have a rope stretched out tightly, with one end firmly anchored and the other end held by your friend. When your friend moves their hand up and down, a wave is created that travels along the rope from one end to the other. The wave will reflect back and forth between the two ends, causing interference patterns to emerge. This interaction between the incoming and reflected waves leads to the formation of what we call a standing wave. Unlike other waves that move through space, a appears to be "standing still" in its overall pattern.
These patterns are formed by the superposition of two or more waves moving in opposite directions. In a standing wave, certain points along the rope appear to be fixed, called , where the rope doesn't move at all. These nodes are formed by destructive interference, where the crest of the incoming wave aligns with the trough of the reflected wave, canceling each other out. In contrast, there are other points along the rope where the motion is the greatest, called . These are formed by constructive interference, where the crests of the incoming and reflected waves align, resulting in a larger amplitude. An example of a standing wave with 2 nodes and 1 antinode can be seen in Figure 5.
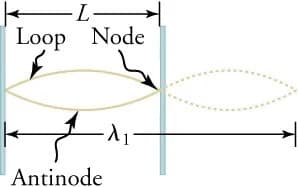
Figure 5: Standing wave with nodes and antinodes shown (OpenStax, 2020).
The formation of a standing wave requires the presence of two waves with the same frequency, wavelength, and amplitude travelling in opposite directions along the same medium. As the waves meet and interfere, their peaks and troughs align in a way that produces a stable pattern. These patterns depend on the length of the rope and the frequency of the wave. Only certain wavelengths can fit perfectly between the fixed ends, resulting in distinct standing wave patterns, as seen in Figure 6.
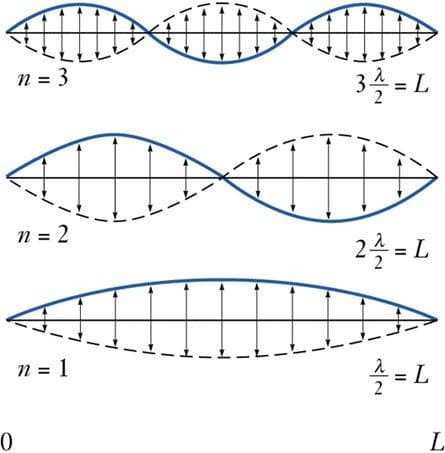
Figure 6: Different standing wave patterns (Toppr).
Standing waves occur in nature and have practical applications in various fields. One example of standing waves can be seen when looking at the surface of a glass of milk in a refrigerator. The vibrations from the refrigerator motor create waves on the milk that oscillate up and down but do not seem to move across the surface. The two waves that produce standing waves are due to the reflections from the side of the glass. Another example are the standing waves created by the constructive and destructive interference of seismic waves from earthquakes. As the earthquake waves travel along the surface of the Earth and reflect off denser rocks, constructive interference occurs at certain points. As a result, areas closer to the epicenter are not damaged while areas farther from the epicenter are.
Lesson 3: Reflection and Refraction
Relection and Refraction of Waves
When a guitarist plucks a string, it starts to vibrate and creates a wave that travels along the string. This wave reaches the end of the string where it encounters an obstacle like the guitar's bridge or a fret. At this point, two things can happen: reflection and refraction.
First, let's talk about . When the wave reaches the obstacle, it reflects back toward the source, just like when you see your reflection in a mirror. In the case of the guitar string, this reflected wave travels back along the string and combines with the incoming wave. This interaction between the two waves creates a standing wave pattern, with nodes and antinodes as we discussed earlier. The reflection of the wave is responsible for setting up this stationary pattern on the string. As the wave is reflected, the wave experiences an inversion, which means that it flips vertically, as seen in Figure 9. If a wave hits the fixed end with a crest, it will return as a trough, and vice versa.
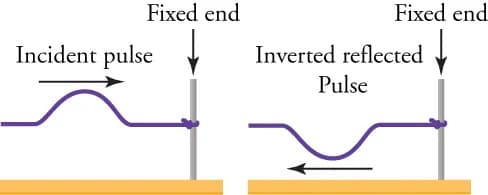
Figure 10: A wave is inverted after reflection from a fixed end (Open Stax, 2020).
If the end of the string is not fixed, it is said to be a free end, and no inversion occurs. When the end is loosely attached, it reflects without inversion, and when the end is not attached to anything, it does not reflect at all.
Now, let's move on to . Refraction occurs when the wave encounters a change in medium, such as when the guitar string passes over a fret. At this point, the speed of the wave changes because the tension and density of the string differ on either side of the fret. As a result, the wavelength and direction of the wave are also altered. When the wave passes over the fret, it bends or changes direction due to the change in speed. It's similar to how a fish appears to be in a different place, as seen in Figure 8. Refraction can cause the wave to spread out or concentrate, depending on the angle at which it enters the new medium.
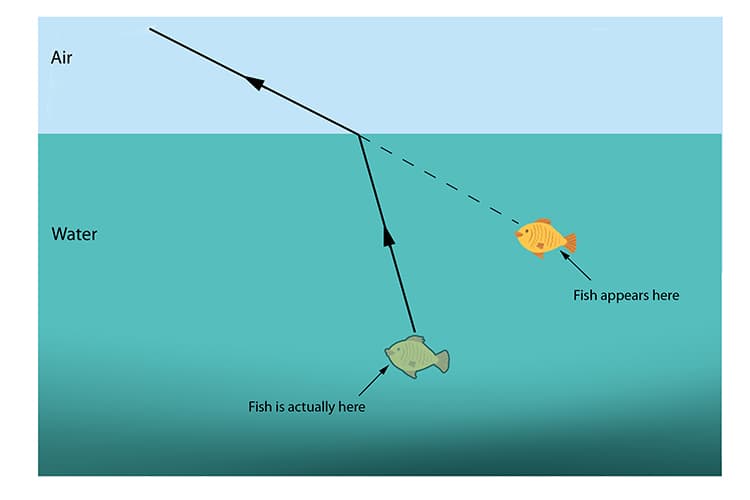
Figure 11: When you see a fish in the water, the light wave refracts so that the fish looks to be in a different position than it actually is (Mammoth Memory).
In the case of a guitar string, the refraction of the wave can affect the pitch or frequency of the sound produced. As the wave passes over different frets, the effective length of the vibrating string changes, altering the standing wave pattern and producing different musical notes.