Section 3: Sound Waves
Section Learning Outcomes:
Section Key Terms:
Bored Already? Press the buttons to dive into applications!
Lesson 1: Properties of Sound Waves
Sound Waves
Sound waves are all around us, shaping the world we perceive through our ears. Have you ever wondered how we hear the music playing on a radio, the voice of a friend, or the crashing of ocean waves? It's all thanks to the fascinating phenomenon of sound waves. are vibrations that travel through a medium, such as air or water, creating a chain reaction of particles passing energy from one to another. Just like how a pebble creates ripples in a pond, the vibrations produced by sound sources generate waves that spread out in all directions.
If a guitar string is plucked it will vibrate and produce a sound wave. As the string oscillates back and forth, part of the string's energy goes into compressing and expanding the surrounding air. This creates regions of slightly higher and lower pressures. The higher-pressure regions where the particles are densely packed together are referred to as , while the lower-pressure regions where the particles are spread apart are known as . An example of compressions and rarefactions being produced can be seen in Figure 1. The vibration of the string produces a pressure disturbance that moves through the air as longitudinal waves with the same frequency as the string. The areas of compression and rarefaction are analogous to the crests and troughs in transverse waves.
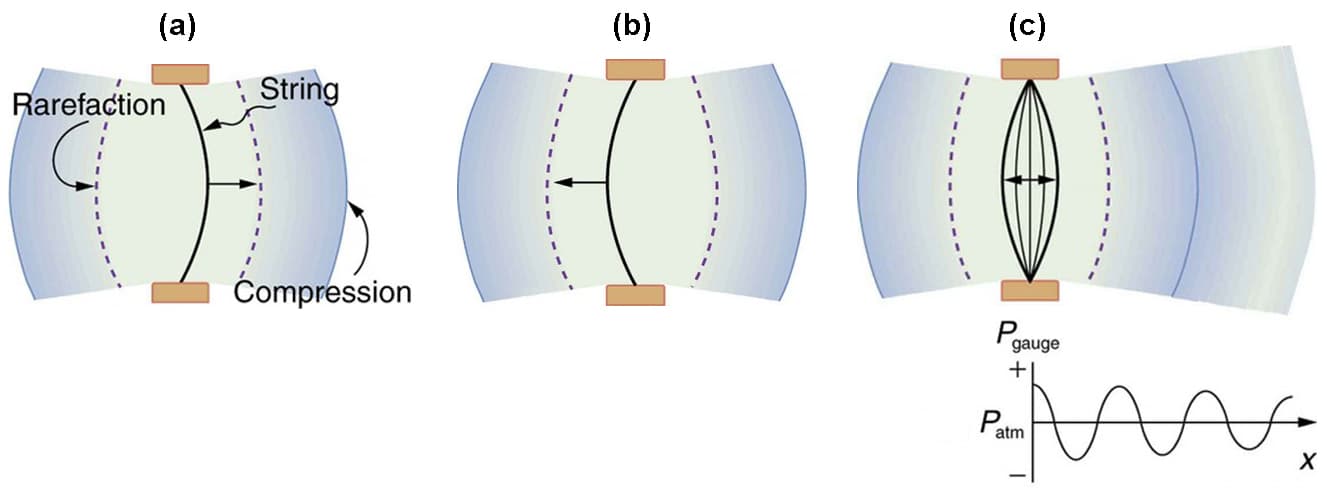
Figure 1: (a) A vibrating string moving to the right compresses the air in front of it and expands the air behind it. (b) As the string moves to the left, it creates another compression and rarefaction as the ones on the right move away from the string. (c) After many vibrations, there is a series of compressions and rarefactions moving out from the string as a sound wave. The graph shows gauge pressure versus distance from the source. Pressures vary only slightly from atmospheric for ordinary sounds (Lumens Learning).
As a sound wave travels from its source, its amplitude decreases with distance because the energy of the wave is spread over a larger and larger area. When the sound wave makes contact an object like the eardrum, some energy is absorbed by the object, while other energy is converted to thermal energy in the air.
The Speed of Sound
The speed of sound refers to how quickly sound waves propagate through a medium, such as air, water, or glass. The speed of sound in a medium is influenced by the medium's rigidity (or compressibility in gases) and its density. In general, sound travels faster in the less dense and more elastic (or more rigid or less compressible) medium.
In dry air at room temperature (around 20 degrees Celsius), sound travels at approximately 343 m/s. This is low in comparison because air is compressible. This speed can vary slightly depending on factors such as temperature, humidity, and atmospheric pressure. In liquids and solids, sound travels faster than in air due to the increased density of the materials and thus the closer proximity of particles.
Lesson 2: The Speed of Sound and Properties of Sound Waves
The Relationship between Speed, Frequency, and Wavelength
As we learned above, sound waves travel at different speeds through different media and just like other waves, sound waves have a specific frequency and wavelength associated with them. If you have ever viewed a fireworks display, you may have noticed that the flash of the explosion is seen before its sound is heard. This is because sound travels much slower than light.
The relationship between the speed of sound, its frequency, and wavelength is the same as for all waves:
where v is the speed of sound in meters per second (m/s), f is its frequency in Hertz (Hz), and λ is its wavelength in meters (m).
Recall that wavelength is defined as the distance between adjacent identical parts of a wave. The wavelength of a sound wave, therefore, is the distance between adjacent identical parts of a sound wave, such as compressions or rarefactions. Just as the distance between adjacent crests in a transverse wave is one wavelength, the distance between adjacent compressions in a sound wave is also one wavelength, whereas the frequency of a sound wave is the same as that of the source. For example, a tuning fork vibrating at a given frequency would produce sound waves that oscillate at that same frequency.
One of the most important properties of sound is that its speed is nearly independent of frequency. If this were not the case, and high-frequency sounds traveled faster, for example, then the farther you were from a band in a football stadium, the more the sound from the low-pitch instruments would lag behind the high-pitch ones. But we know the music from all instruments arrives in cadence independent of distance, thus all frequencies must travel at nearly the same speed. Recall that v=fλ, and in a given medium under fixed temperature and humidity, v is constant. Therefore, the relationship between f and λ is inverse: the higher the frequency, the shorter the wavelength of a sound wave.
The speed of sound can change when sound travels from one medium to another. However, the frequency usually remains the same because it is determined by the vibrations of the source and is not affected by the medium through which the sound is traveling. If v changes and f remains the same, then the wavelength λ must change.
The Speed of Sound and Temperature
If we now consider that temperature can affect the speed of sound, it can be seen that as the temperature of a medium increases, the speed of sound also increases. This relationship can be explained by considering the properties of the medium at different temperatures. Sound travels through a medium by causing particles to vibrate and transmit energy. In a gas, such as air, the particles are constantly in motion due to their thermal energy. As the temperature increases, the particles' motion becomes more vigorous, leading to an increased collision frequency and an enhanced transmission of sound energy, resulting in a higher speed of sound.
The Newton-Laplace equation provides an approximate estimation of the speed of sound in air as a function of temperature:
where v is the speed of sound in m/s at temperature T in Kelvin (K) and v0 is the speed of sound at a reference temperature T0. The reference temperature, T0, is most often taken to be 273.15 K (0 degrees Celsius). At this reference temperature, the speed of sound in dry air is approximately 331.4 m/s.
Lesson 3: Sound Intensity and Sound Level
Amplitude, Loudness, and Energy of a Sound Wave
In a quiet forest, you can sometimes hear a single leaf fall to the ground whereas in a traffic jam filled with honking cars, you may have to shout just so the person next to you can hear. The loudness of a sound is related to how energetically its source is vibrating.
A useful quantity for describing the loudness of sounds is called . In general, the intensity of a wave is the power per unit area carried by the wave, where the power P is the rate at which energy is transferred by the wave. In equation form, the intensity I in Watts per meters squared (m/s2) is
The intensity of a sound also depends upon its pressure amplitude in Pascals (P=N/m2), the density of the material ρ in kg/m3, and the speed of sound in the medium vw in m/s. The relationship between the intensity of a sound wave and its pressure amplitude (or pressure variation ΔP) is
The Decibel Scale
When people talk about the loudness of a sound, they often describe it in units of rather than Watts per meter squared (W/m2). While sound intensity (in W/m2) is in the SI unit, the in decibels (dB) is more a convenient and relevant way to express the wide range of sound levels that humans can perceive, from the faintest whisper to the loudest rock concert. The way our ears perceive sound can be more accurately described by the logarithm of the intensity of a sound rather than the intensity of a sound. The sound intensity β is defined to be
where I is the sound intensity in W/m2, and I0=10-12 W/m2 is a reference intensity. I0 is chosen as the reference point because it is the lowest intensity of sound a person with normal hearing can perceive. The threshold of human hearing is 0 decibels or I=10-12 W/m2.
On the decibel scale, an increase of 10 dB is generally perceived as roughly doubling the loudness. A 20 dB increase is perceived as approximately four times louder, and so on. For example, a 90 dB sound compared with a 60 dB sound is 30 dB greater, or 103 times as intense.
Since β is defined in terms of a ratio, it is unitless. The unit called decibel (dB) is used to indicate that this ratio is multiplied by 10. The sound intensity level is not the same as sound intensity - it tells you the level of the sound relative to a reference intensity rather than the actual intensity.
When a sound wave reaches a listener's ear, the sound is interpreted by the brain as loud or soft, depending on the intensity of the wave, with higher intensities giving rise to louder sounds. However, the relation between intensity and loudness is not a simple proportionality, because doubling the intensity does not double the loudness.
Suppose you are sitting in front of a stereo system that is producing an intensity level of 90 dB. If the volume control on the amplifier is turned up slightly to produce a 91 dB level, you would just barely notice the change in loudness. Hearing tests have revealed that a 1 dB change in the intensity level corresponds to approximately the smallest change in loudness that an average listener with normal hearing can detect. Since 1 dB is the smallest perceivable increment in loudness, a change of 3 dB - say, from 90 to 93 dB - is still a rather small change in loudness.