Section 1: Types of Waves
Section Learning Outcomes:
Section Key Terms:
Bored Already? Press the buttons to dive into applications!
Lesson 1: Introduction to Waves
Mechanical Waves
Picture a sunny day at the beach with ocean waves, one after another, rolling towards the beach, rising and falling with a rhythmic motion. Each wave carries a sense of power and grace as it crashes onto the shore, releasing a spray of droplets that glisten in the sunlight. The sound of the crashing waves echoes in your years, creating a soothing symphony that reverberates along the coast.
After watching the waves for a few minutes, you take out the stopwatch on your phone and start to measure the time between wave crashes, noticing that the waves arrive after the same amount of time without much delay. These ocean waves are not the only ones in nature, and they are not alone in exhibiting this periodic behaviour. The music coming out of the portable speaker on your cooler produces sound waves that allow you to hear the lyrics and beats. The beautiful, refreshing sunlight beaming down onto your skin, tanning it, are light waves that transmit electromagnetic radiation and allow us to see everything around the beach, including the ocean waves crashing onto the shore.
can be described as disturbances that propagate energy through a medium or even through empty space. They are the result of a rhythmic back-and-forth motion, a dance between forces and matter. As the wind blows across the surface of the ocean, it imparts energy to the water, creating a ripple that begins to travel. This ripple gradually grows in size and momentum, transforming into a fully formed wave, ready to make its journey toward the shore.
Ocean waves, as well as other waves, such as the seismic wave produced by an earthquake or the sound waves from your speaker, are examples of that require a medium to travel/propagate. The that is needed for these mechanical waves may be a solid such as the Earth's crust, a liquid such as the water in the ocean, or a gas such as the air.
Electromagnetic Waves
The light waves from the Sun exhibit the same properties as mechanical waves but unlike mechanical waves, they do not require a medium to travel. Light waves are a type of that can travel through a vacuum such as the empty parts of outer space. The X-rays used in computed tomography (CT) scans, the gamma rays used to treat cancer, and the radio waves that transmit text messages and other information across the world, are all examples of how we have harnessed electromagnetic waves to benefit society. Electromagnetic waves are classified by their wavelength, frequency, and energy associated with the wave, all properties that will be discussed later in this lesson. This classification of waves is known as the electromagnetic spectrum and is shown in Figure 1.
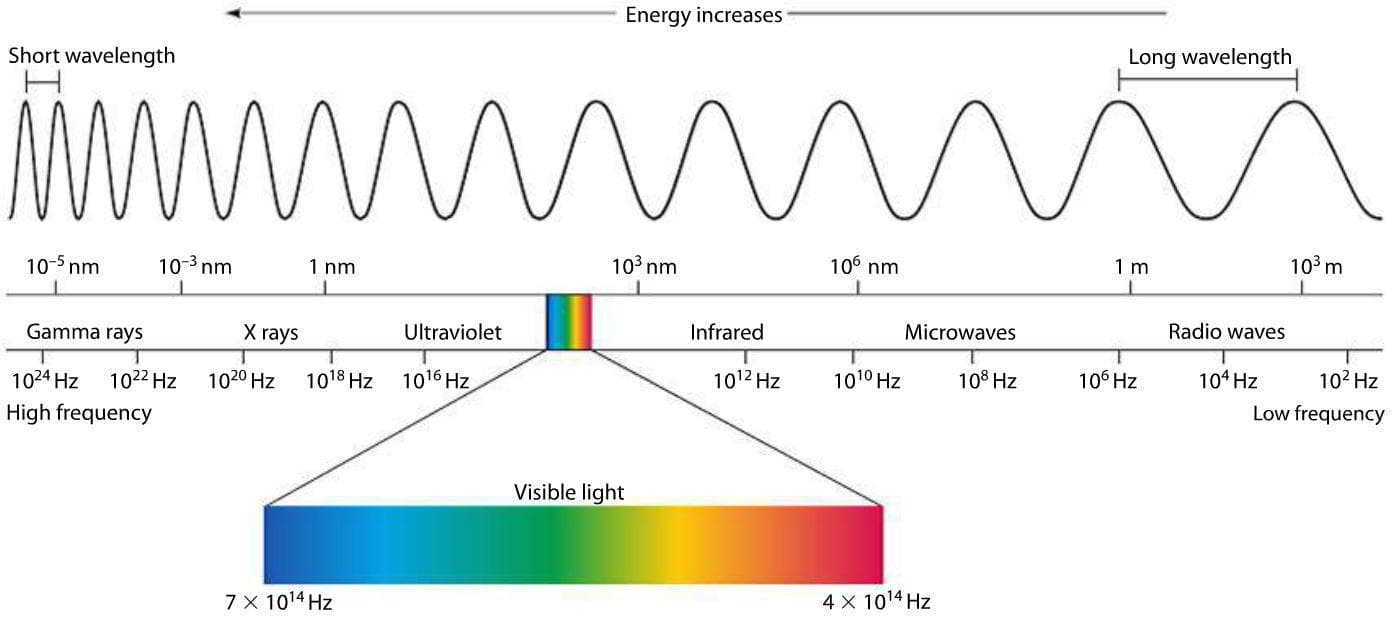
Figure 1: The electromagnetic spectrum shows the major categories of electromagnetic waves including radio waves, microwaves, infrared radiation, visible light, ultraviolet light, x-rays, and gamma rays (Mini Physics, 2016).
Periodic Waves
Let's return to our early discussion on ocean waves. After taking multiple measurements to find the time between the crashes of the waves, you determine that the waves arrive at the shore after the same amount of time without much delay. This occurs because ocean waves are continuous and have a specific period, even if they do not seem to be. Ocean waves are known as since they repeat at regular intervals of time and space with the same shape and pattern. The light waves from the Sun and the electricity powering your homes also exhibit a periodic behaviour just like ocean waves.
The waves in a wave pool are a perfect way to visualise the periodic nature of these waves. They repeat in a designated cycle and are associated with a phenomenon known as simple harmonic motion. The periodic motion of the wave causes each particle in the water to move back and forth periodically through the same position. As the wave moves, it starts to look like a series of identical crests and troughs, as seen in Figure 6. The uppermost position of the wave, the crest, and the lowest position of the wave, the trough, will always be the same height and appear repeatedly after the period has passed. The distance between two consecutive crests or troughs is called the .
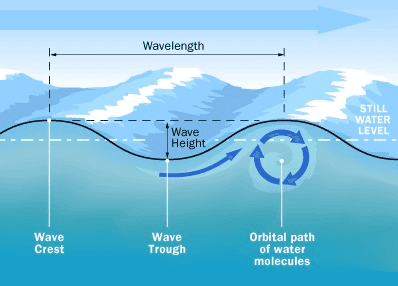
Figure 6: Ocean wave schematic showing the wavelength, and wave crests and troughs with respect to the still water level (Mike Eat Sea).
If you observe the motion of a single crest or trough, you will notice that it moves up and down in a regular pattern. This repetitive motion occurs at a specific , which refers to the number of wave cycles passing by a point in a given time. The time between crests is called the wave's , which represents the time it takes for one complete wave cycle to pass by a specific point.
Pulse Waves
Now imagine gently plucking a guitar string. As you release it, the string moves back and forth rapidly, creating a disturbance or a pulse. This pulse travels along the string from the point where it was plucked towards both ends. The string momentarily bends and then returns to its original position, transferring energy along its length. The wave on the guitar string that is produced is known as a and it consists of a single crest, representing the highest point of displacement, followed by a trough, representing the lowest point. As the pulse propagates through the string, it carries energy but does not repeat itself in a regular pattern, as seen in Figure 7.
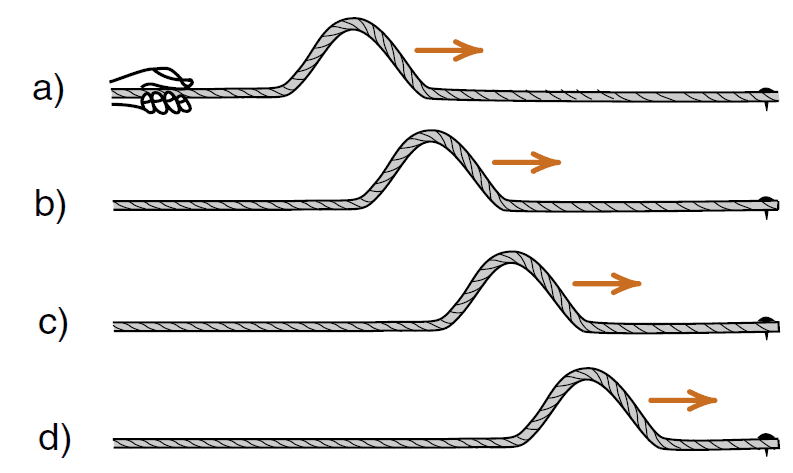
Figure 7: Pulse wave on a string moving over time from (a) to (d) (Almerja.com, 2020).
Unlike periodic waves, which have repeating patterns of crests and troughs, pulse waves are singular events that occur once and then gradually diminish. In the case of a guitar string, the pulse quickly spreads along the string, causing it to vibrate with a distinct sound. However, the pulse does not continue to repeat itself like a continuous oscillation.
Longitudinal Waves
All mechanical waves fall into one of three categories depending on their type of motion: transverse, longitudinal, or torsional. , also known as compression or compressional waves, are a type of mechanical wave where the particles of the medium vibrate back and forth in the same direction as the wave propagation, as seen in Figure 8.
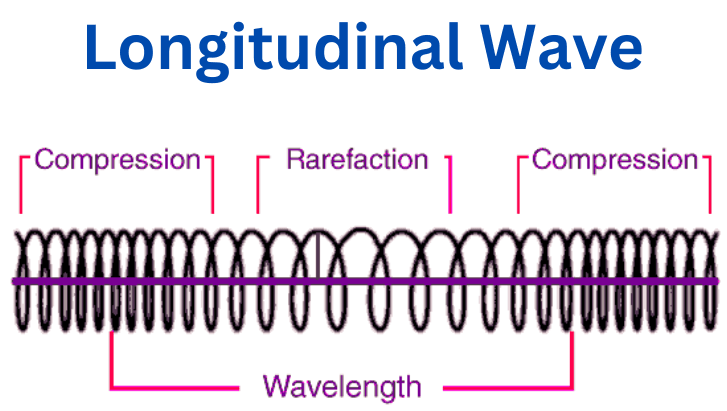
Figure 8: Longitudinal wave on a spring showing compressions and rarefactions as the longitudinal wave move through the spring (Edu Input).
An excellent example of a longitudinal wave is ultrasound. Ultrasound waves are sound waves with frequencies higher than the upper limit of human hearing, typically above 20,000 hertz (Hz). These waves are generated by a transducer, which converts electrical energy into mechanical vibrations. The transducer emits high-frequency sound waves that travel through a medium, such as air or water.
As ultrasound waves propagate through the medium, they cause the particles of the medium to vibrate parallel to the direction of wave travel. These compressions and rarefactions of the particles form areas of high-pressure and low-pressure regions, respectively. In other words, the particles in the medium undergo longitudinal displacement, moving back and forth in the same direction as the wave.
The energy carried by ultrasound waves enables them to penetrate through various materials, including human tissues. In medical applications, ultrasound is widely used for imaging internal organs, monitoring pregnancies, and diagnosing conditions. When an ultrasound scan is performed, the transducer sends out a series of ultrasound waves into the body. These waves bounce off the tissues and organs inside and return to the transducer.
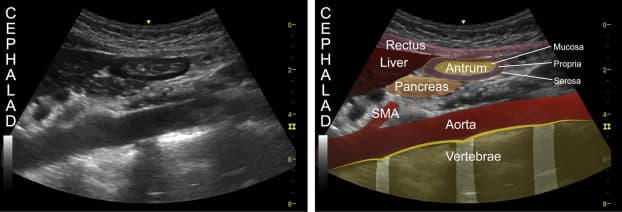
Figure 9: Ultrasound image of the abdomen showing the liver, pancreas, rectus, antrum, aorta, and more (BJA Education, 2019).
By analyzing the time it takes for the ultrasound waves to travel back to the transducer and the changes in their frequency, a computer system can create real-time images or sonograms of the internal structures, as seen in Figure 9. These images provide valuable information about the size, shape, and condition of organs, as well as the presence of any abnormalities or diseases.
Transverse Waves
Imagine holding one end of a taut rope and moving your hand up and down in a regular pattern. As your hand moves upward, it creates a crest, or a peak, in the string. Conversely, as your hand moves downward, it creates a trough, or a dip, in the string. These crests and troughs form the characteristic shape of the wave. The waves that are created on the string are known as (or shear waves) and they are a type of mechanical wave where the particles of the medium vibrate perpendicular to the direction of wave propagation.
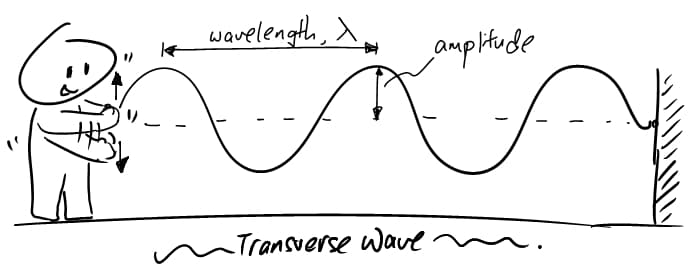
Figure 11: Transverse wave created on a rope with one end fixed to the wall (Socratic Q&A).
In a transverse wave on a rope, the particles of the string move perpendicular to the direction of the wave, as seen in Figure 11. While the wave itself moves horizontally along the string, the individual particles of the string move vertically, oscillating up and down as the wave passes through. The particles do not move along with the wave; they only vibrate in place.
Light waves and the ripples on the surface of water are also examples of transverse waves. In the case of light, the wave consists of oscillating electric and magnetic fields that are perpendicular to the direction of wave propagation, as seen in Figure 12. This enables light to exhibit properties such as polarization, where the oscillations occur in a specific plane.
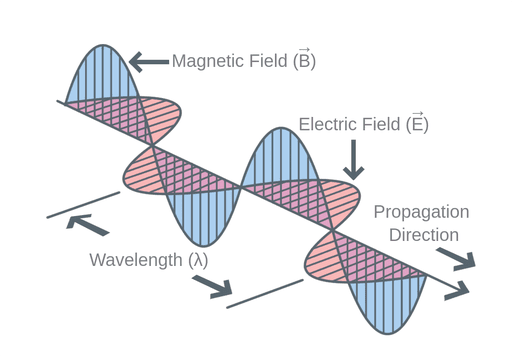
Figure 12: The electric and magnetic oscillating field vectors of an electromagnetic wave (Labster Theory).
Torsional Waves
Now let's take the same rope as above when demonstrating transverse waves and twist one end while holding the other end taut. The twisted portion moves along the length of the rope, while the particles of the rope oscillate back and forth around their equilibrium position. As the wave travels, the twist is transferred from one particle to the next, resulting in a wave-like motion, as seen in Figure 13.

Figure 13: Torsional wave in a rope.
When we twist the one end of the rope, a is generated, propagating along the length of the rope. However, unlike transverse waves where particles move perpendicular to the direction of wave propagation, in the case of torsional waves, the particles oscillate around an axis parallel to the direction of wave propagation.
An everyday example of torsional waves is seen in the transmission of rotational motion in vehicles. In a car or a bicycle, the engine generates rotational motion that is transmitted through a series of rotating shafts and gears. These rotational motions travel as torsional waves, enabling the power to be transmitted efficiently from the engine to the wheels.
Lesson 2: Wave Properties
Wave Variables
To explain the properties of a wave, let's consider the scenario of throwing a pebble into a calm pond. This example will help us understand some key properties of waves.
As the pebble hits the surface of the water, it creates a disturbance that radiates outward in the form of circular ripples. The distance between two consecutive crests or troughs of these ripples represents the of the wave. You can observe that the ripples are spaced evenly apart, forming a pattern of peaks and valleys. You can also count the number of crests passing a fixed point, such as a leaf on the water's surface, within a specific timeframe. This count corresponds to the of the waves generated by the pebble. The frequency refers to the number of complete oscillations, or cycles, that occur in a given time period.
The is the maximum displacement of the water particles from their undisturbed position. In the scenario of the pebble being thrown into a calm pond, you'll notice that the height of the ripples, or the distance between the undisturbed water level and the crest or trough, represents the amplitude. The larger the disturbance created by the pebble, the higher the amplitude of the resulting waves. You can also observe the waves travelling across the surface of the water at a certain speed. By measuring the distance the waves cover in a given time, you can calculate the .
These characteristics can be visualised by looking at the idealised water wave in Figure 17 with the wavelength is described by the variable λ, the amplitude by X, and the wave velocity by vw.
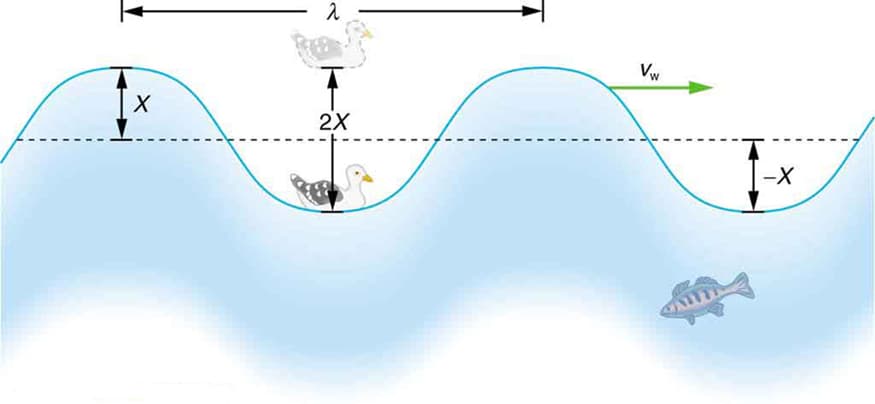
Figure 17: An idealized ocean wave with wavelength λ, amplitude X, and wave velocity vw (OpenStax, 2020).
The Relationship between Wave Frequency, Period, Wavelength, and Wave Velocity
The wave velocity vw can be determined if you know the wavelength and frequency of the wave. Just as in the case of harmonic motion of an object, the relationship between the frequency and period of a wave is
where f is the frequency of the wave in Hertz (Hz) and T is the period of the wave in seconds (s). It can be seen from this relationship that a higher frequency means a shorter period since the two are inversely related.
The wave velocity is the distance the wave travels in a given time, which is one wavelength in a time of one period. In equation form it is written as
where λ is the wavelength of the wave in meters (m). This relationship is known as the universal wave equation and it can be seen that in a medium where vw is constant, the higher the frequency, the smaller the wavelength.