Section 5: Sound Interference and Resonance

Lesson 1: Resonance and Beats

Resonance

The Tacoma Narrows Bridge incident stands as a captivating testament to the power of resonance. In 1940, this suspension bridge in Washington State began to sway and twist in an otherworldly dance, ultimately leading to its dramatic collapse. The bridge's demise was triggered by the perfect alignment of wind forces with its natural frequency, resulting in a mesmerizing display of resonance. This extraordinary event serves as a striking example of how the interplay between external forces and an object's inherent vibrations can have catastrophic consequences.

Figure 1: Tacoma Narrows Bridge collapse in 1940 (Britannica).

Most of us have played with toys where an object bobs up and down on an elastic band, something like the paddle ball suspended from a finger in Figure 2. At first you hold your finger steady, and the ball bounces up and down with a small amount of damping. If you move your finger up and down slowly, the ball will follow along without bouncing much on its own. As you increase the frequency at which you move your finger up and down, the ball will respond by oscillating with increasing amplitude. When you drive the ball at its natural frequency, the ball's oscillations increase in amplitude with each oscillation for as long as you drive it. As the driving frequency gets progressively higher than the resonant or natural frequency, the amplitude of the oscillations becomes smaller, until the oscillations nearly disappear and your finger simply moves up and down with little effect on the ball.

Figure 2: Paddle ball.

Resonance can occur in various systems, including mechanical, acoustic, and electromagnetic systems. It is observed in musical instruments, where the strings or air columns vibrate at their natural frequencies in response to external forces, resulting in the production of sound. Resonance is also utilised in engineering applications such as in electrical engineering to adjust/tune the circuits to resonate at specific frequencies.

However, resonance can have both beneficial and detrimental effects. In some cases, resonance can enhance the performance of a system, as in the case of musical instruments producing rich and loud sounds. On the other hand, if the external force continues to be applied at the resonant frequency and the system cannot dissipate the energy, it can lead to unwanted vibrations and potential damage. This is evident when analysing the Tacoma Narrows Bridge example, where the strong winds caused excess vibrations and eventually led to the bridge collapsing.

Beats

$$f_B=|f_1-f_2|$$

2here f₁ and f₂ are the frequencies of the two original waves and f_B is the beat frequency. If the two frequencies of sound waves are similar, then what we hear is an average frequency that gets louder and softer at the beat frequency.

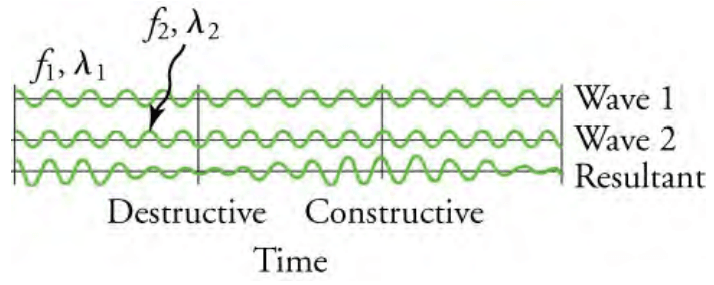
Figure 3: Beats are produced by the superposition of two waves of slightly different frequencies but identical amplitudes. The waves alternate in time between constructive interference and destructive interference, giving the resulting wave a time-varying amplitude (OpenStax, 2020).

Lesson 2: Fundamental Frequency and Harmonics

Fundamental Frequencies and Harmonics

Suppose we hold a tuning fork near the end of a tube that is closed at the other end, as shown in Figure 4, Figure 5, and Figure 6. If the tuning fork has just the right frequency, the air column in the tube will resonate loudly, but at most frequencies, it only vibrates very little. This means that the air column has only certain natural frequencies. If the tuning fork vibrates at the right frequency, say the lowest of the air column’s natural frequencies, a disturbance will travel down the tube at the speed of sound and will bounce off the closed end of the tube, as seen in the figures. If the tube is just the right length, the reflected sound arrives back at the tuning fork exactly half a cycle later, and it interferes constructively with the continuing sound produced by the tuning fork. The incoming and reflected sounds form a standing wave in the tube and the air column resonates.

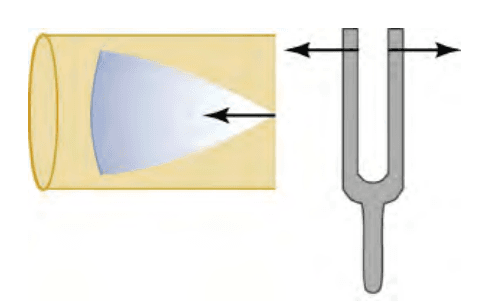
Figure 4: Resonance of air in a tube closed at one end, caused by a tuning fork. A disturbance moves down the tube (OpenStax, 2020).

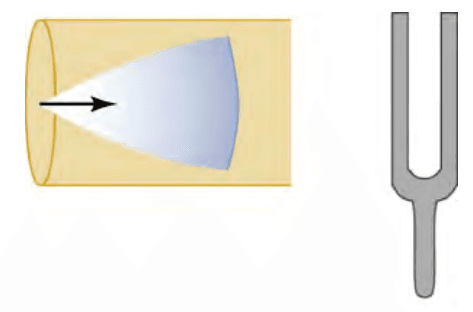
Figure 5: Resonance of air in a tube closed at one end, caused by a tuning fork. The disturbance reflects from the closed end of the tube (OpenStax, 2020).

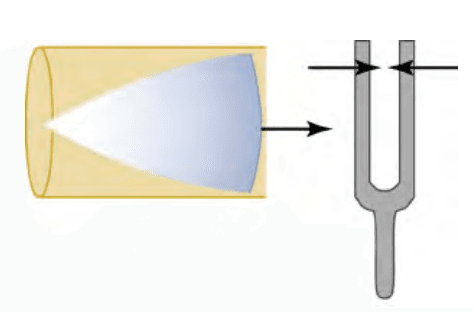
Figure 6: Resonance of air in a tube closed at one end, caused by a tuning fork. If the length of the tube is just right, the disturbance gets back to the tuning fork half a cycle later and interferes constructively with the continuing sound from the tuning fork. This interference forms a standing wave, and the air column resonates (OpenStax, 2020).

The standing wave formed in the tube has its maximum air displacement (an antinode) at the open end and no displacement (a node) at the closed end. The motion of the wave at the antinode is unconstrained while it is halted at the node. The distance from a node to an antinode is one-fourth of a wavelength, and this equals the length of the tube; therefore λ = 4L. This same resonance can be produced by a vibration introduced at or near the closed end of the tube, as shown in Figure 7.

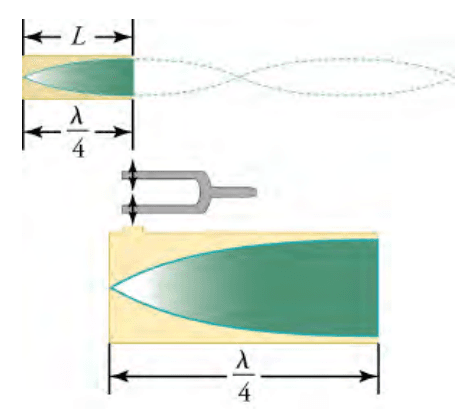
Figure 7: The same standing wave is created in the tube by a vibration introduced near its closed end (OpenStax, 2020).

Since maximum air displacements are possible at the open end and none at the closed end, there are other shorter wavelengths that can resonate in the tube, as shown in Figure 8. Here the standing wave has three-fourths of its wavelength in the tub, or $$L=(3/4)\lambda'$$ so that $$\lambda'=4L/3$$ There is a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube.

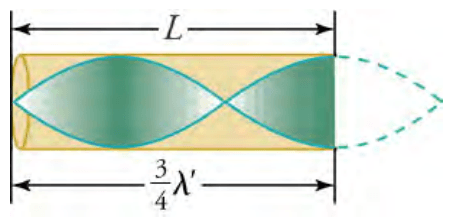
Figure 8: Another response for a tube closed at one end. This has maximum air displacements at the open end, and none at the closed end. The wavelength is shorter, with three-fourths λ’ equaling the length of the tube, so that λ'=4L/3. The higher-frequency vibration is the first overtone (OpenStax, 2020).

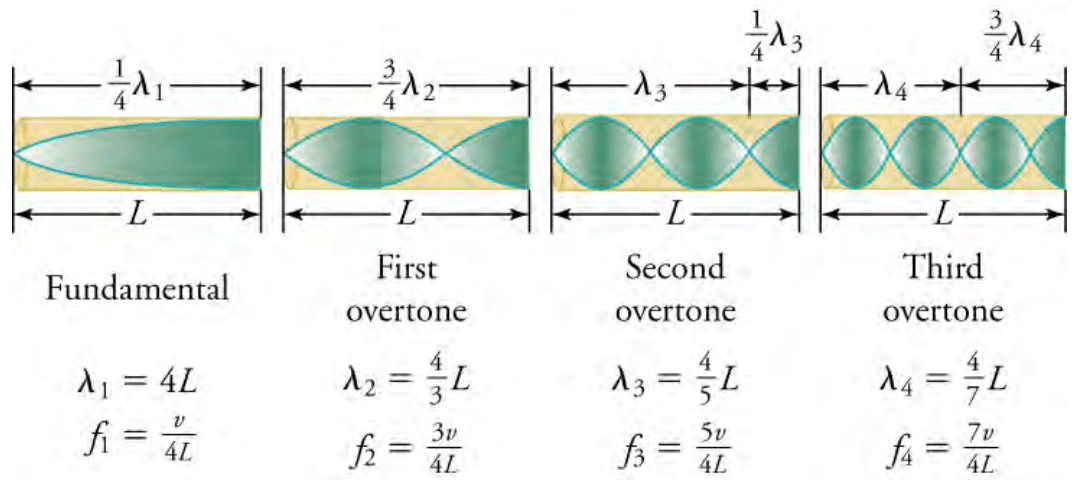
Figure 9: The fundamental and three lowest overtones for a tube closed at one end. All have maximum air displacements at the open end and none at the closed end (OpenStax, 2020).

The fundamental and overtones can be present at the same time in a variety of combinations. For example, the note middle C on a trumpet sounds very different from middle C on a clarinet, even though both instruments are modified versions of a tube closed at one end. The fundamental frequency is the same (and usually the most intense), but the overtones and their mix of intensities are different. This mix is what gives musical instruments (and human voices) their distinctive characteristics, whether they have air columns, strings, or drumheads. Much of our speech is determined by shaping the cavity formed by the throat and mouth and positioning the tongue to adjust the fundamental and combination of overtones.

Open-Pipe and Closed-Pipe Resonators

The resonant frequencies of a tube closed at one end (known as a closed-pipe resonator) are

$$f_n=n\frac{v}{4L}$$

for n=1,3,5, etc, where f₁ is the fundamental, f₃ is the first overtone, and so on. Note that the resonant frequencies depend on the speed of sound v and on the length of the tube L.

Another type of tube that is open at both ends is known as an open-pipe resonator. Examples of open-pipe resonators include organ pipes, flutes, and oboes. The air columns in tubes at both ends have maximum air displacements at both ends, as seen in Figure 10 where the standing waves are shown.

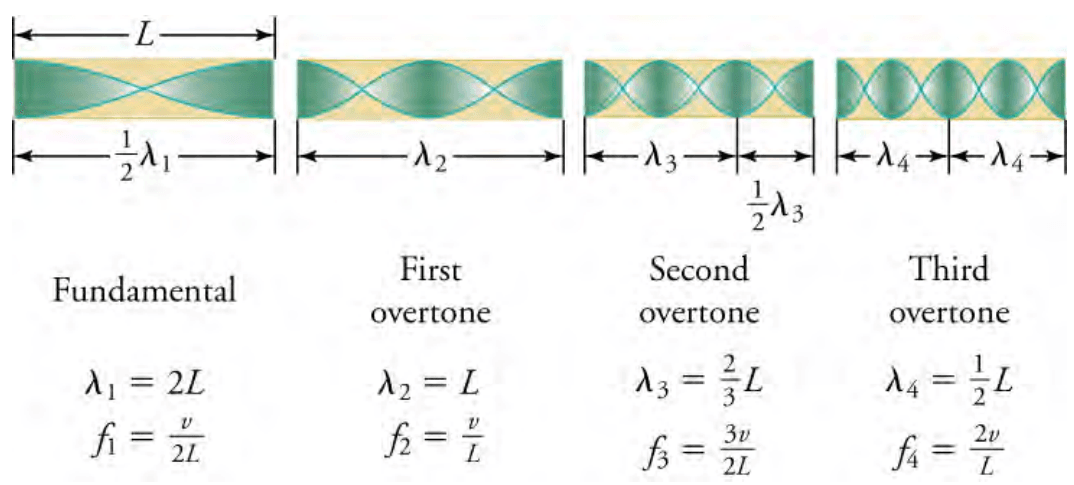
Figure 10: The resonant frequencies of a tube open at both ends are shown, including the fundamental and the first three overtones. In all cases the maximum air displacements occur at both ends of the tube, giving it different natural frequencies than a tube closed at one end (OpenStax, 2020).

The resonant frequencies of an open-pipe resonator are

$$f_n=n\frac{v}{2L}$$

for n=1,2,3, etc, where f₁ is the fundamental, f₂ is the first overtone, f₃ is the second overtone, and so on. Note that a tube open at both ends has a fundamental frequency twice what it would have if closed at one end. It also has a different spectrum of overtones than a tube closed at one end. So if you had two tubes with the same fundamental frequency but one was open at both ends and the other was closed at one end, they would sound different when played because they have different overtones.

Middle C, for example, would sound richer played on an open tube since it has more overtones. An open-pipe resonator has more overtones than a closed-pipe resonator because it has even multiples of the fundamental frequency as well as odd multiples, whereas a closed tube has only odd multiples.